Tabela verdade ou tabela de verdade é uma ferramenta de natureza matemática muito utilizada no campo do raciocínio lógico. Seu objetivo é verificar a validade lógica de uma proposição composta (argumento formado por duas ou mais proposições simples).
Exemplos de proposições compostas:
- João é alto e Maria é baixa.
- Pedro é alto ou Joana é loira.
- Se Pedro é alto, então Joana é ruiva.
Cada uma das proposições compostas acima são formadas por duas proposições simples unidas pelos conectivos em negrito. Cada proposição simples pode ser verdadeira ou falsa e isso implicará diretamente no valor lógico da proposição composta. Se adotarmos a frase “João é alto e Maria é baixa”, as possíveis valorações dessa afirmação serão:
Se João for alto e Maria for baixa, a frase “João é alto e Maria é baixa” é VERDADEIRA.
Se João for alto e Maria não for baixa, a frase “João é alto e Maria é baixa” é FALSA.
Se João não for alto e Maria for baixa, a frase “João é alto e Maria é baixa” é FALSA.
Se João não for alto e Maria não for baixa, a frase “João é alto e Maria é baixa” é FALSA.
Se João for alto e Maria for baixa, a frase “João é alto e Maria é baixa” é VERDADEIRA.
Se João for alto e Maria não for baixa, a frase “João é alto e Maria é baixa” é FALSA.
Se João não for alto e Maria for baixa, a frase “João é alto e Maria é baixa” é FALSA.
Se João não for alto e Maria não for baixa, a frase “João é alto e Maria é baixa” é FALSA.
A tabela verdade esquematiza esse mesmo raciocínio (ver o tópico Conjunção abaixo) de forma mais direta. Além disso, as regras da tabela verdade podem ser aplicadas independente do número de proposições na frase.
Como funciona?
Primeiramente, transformar-se as proposições da questão em símbolos utilizados na lógica. A lista de símbolos universalmente usada é:
Por fim, aplica-se a operação lógica definida pelo conectivo mostrado. Conforme a lista acima, essas operações podem ser: negação, conjunção, disjunção, condicional e bicondicional.Em seguida, monta-se uma tabela com todas as possibilidades de valoração de uma proposição composta, substituindo as afirmações por símbolos. Vale esclarecer que nos casos em que existirem mais de duas proposiçõesr, s, e assim em diante.
, elas poderão ser simbolizadas pelas letras
, elas poderão ser simbolizadas pelas letras
Negação
A negação é simbolizada por ~. A operação lógica da negação é a mais simples e muitas vezes dispensa o uso da tabela verdade. Seguindo o mesmo exemplo, se João é alto (p) dizer que João não é alto (~p) é FALSO, e vice-versa.
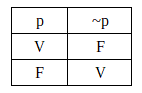
Conjunção
A conjunção é simbolizada por ^. O exemplo "João é alto e Maria é baixa" será simbolizado por "p^q" e a tabela verdade será:
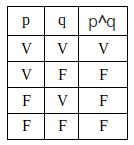
A conjunção sugere uma ideia de acumulação, portanto, se uma das proposições simples for falsa, é impossível que a proposição composta seja verdadeira.
Conclusão: as proposições compostas conjuntivas (que contenham o conectivo e) só serão verdadeiras quando todos os seus elementos forem verdadeiros.
Exemplo:
Paulo, Renato e Túlio são gentis e Carolina é engraçada. - Se Paulo, Renato ou Túlio não forem gentis ou Carolina não for engraçada, a proposição será FALSA. É necessário que todas as informações sejam verdadeiras para que a proposição composta seja VERDADEIRA.
Paulo, Renato e Túlio são gentis e Carolina é engraçada. - Se Paulo, Renato ou Túlio não forem gentis ou Carolina não for engraçada, a proposição será FALSA. É necessário que todas as informações sejam verdadeiras para que a proposição composta seja VERDADEIRA.
Disjunção
A disjunção é simbolizada por v. Trocando o conectivo do exemplo acima para ou teremos "João é alto ou Maria é baixa". Nesse caso, a frase será simbolizada por "pvq" e a tabela verdade será:
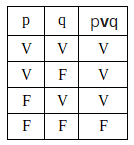
A disjunção implica uma ideia de alternância, portanto, basta que uma das proposições simples seja verdadeira para que a composta também seja.
Conclusão: as proposições compostas disjuntivas (que contenham o conectivo ou) só serão falsas quando todos os seus elementos forem falsos.
Exemplo:
Minha mãe, meu pai ou meu tio me darão um presente. - Para que a afirmação seja VERDADEIRA, basta que apenas um entre a mãe, pai ou tio dê o presente. A proposição só será FALSA caso nenhum deles o dê.
Minha mãe, meu pai ou meu tio me darão um presente. - Para que a afirmação seja VERDADEIRA, basta que apenas um entre a mãe, pai ou tio dê o presente. A proposição só será FALSA caso nenhum deles o dê.
Condicional
A condicional é simbolizada por →. É expressa pelos conectivos se e então, que interligam as proposições simples em uma relação de causalidade. O exemplo "Se Paulo é carioca, então ele é brasileiro" se torna "p→q" e a tabela verdade será:
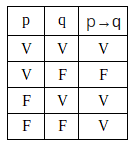
As condicionais possuem uma proposição antecedente e outra consequente, separadas pelo conectivo então.
Na análise das condicionais, é necessário avaliar quais os casos em que a proposição pode ser possível,
considerando a relação de implicação entre a antecedente e a consequente.
Na análise das condicionais, é necessário avaliar quais os casos em que a proposição pode ser possível,
considerando a relação de implicação entre a antecedente e a consequente.
Conclusão: As proposições compostas condicionais (que contenham os conectivos se e então) só serão falsas se a primeira proposição for verdadeira e a segunda falsa.
Exemplo:Se Paulo é carioca, então ele é brasileiro. - Para que esta proposição seja considerada VERDADEIRA, é necessário avaliar os casos em que ela é POSSÍVEL. De acordocom a tabela verdade acima, temos:
Paulo é carioca / Paulo é brasileiro = POSSÍVELPaulo é carioca / Paulo não é brasileiro = IMPOSSÍVEL
Paulo não é carioca / Paulo é brasileiro = POSSÍVEL
Paulo não é carioca / Paulo não é brasileiro = POSSÍVEL
Paulo é carioca / Paulo é brasileiro = POSSÍVELPaulo é carioca / Paulo não é brasileiro = IMPOSSÍVEL
Paulo não é carioca / Paulo é brasileiro = POSSÍVEL
Paulo não é carioca / Paulo não é brasileiro = POSSÍVEL
Bicondicional
A bicondicional é simbolizada por ↔. É lida através dos conectivos se esomente se, que interligam as proposições simples em uma relação de equivalência. O exemplo "João fica feliz se e somente se Maria sorri." se torna "p↔q" e a tabela verdade será:
As bicondicionais sugerem uma ideia de interdependência. Como o próprio nome demonstra, a bicondicional é composta por duas condicionais: uma que parte de p para q (p→q) e outra no sentido contrário (q→p).
Conclusão: As proposições compostas bicondicionais (que contenham os conectivos se e somente se) só serão verdadeiras quando todas as proposições forem verdadeiras, ou todas as proposições forem falsas.
Exemplo:
João fica feliz se e somente se Maria sorri. - Significa dizer que:
Se João fica feliz, Maria sorri e se Maria sorri, João fica feliz =VERDADEIRO
Se João não fica feliz, Maria não sorri e se Maria não sorri, João não fica feliz = VERDADEIRO
Se João fica feliz, Maria não sorri = FALSO
Se João não fica feliz, Maria sorri = FALSO
João fica feliz se e somente se Maria sorri. - Significa dizer que:
Se João fica feliz, Maria sorri e se Maria sorri, João fica feliz =VERDADEIRO
Se João não fica feliz, Maria não sorri e se Maria não sorri, João não fica feliz = VERDADEIRO
Se João fica feliz, Maria não sorri = FALSO
Se João não fica feliz, Maria sorri = FALSO
Resumo geral
É comum que os estudiosos da tabela verdade memorizem as conclusões de cada uma das operações lógicas. Para economizar tempo na resolução de questões, tenha sempre em mente que:
Proposições Conjuntivas: Só serão verdadeiras quando todos os elementos forem verdadeiros.
Proposições Disjuntivas: Só serão falsas quando todos os elementos forem falsos.
Proposições Condicionais: Só serão falsas quando a primeira proposição for verdadeira e a segunda falsa.
Proposições Bicondicionais: Só serão verdadeiras quando todos os elementos forem verdadeiros, ou todos os elementos forem falsos.
Proposições Conjuntivas: Só serão verdadeiras quando todos os elementos forem verdadeiros.
Proposições Disjuntivas: Só serão falsas quando todos os elementos forem falsos.
Proposições Condicionais: Só serão falsas quando a primeira proposição for verdadeira e a segunda falsa.
Proposições Bicondicionais: Só serão verdadeiras quando todos os elementos forem verdadeiros, ou todos os elementos forem falsos.









0 comentários:
Postar um comentário